拉格朗日乘子法（二）

Joseph Louis Lagrange

多个约束条件

引言

现在我们来看看，在一般情况下，当我们在 k个约束条件下：$g_i(x_1, …, x_n) = 0$，其中 $i$ 从 $1$到$k$ ，求最小化 $n$个变量的函数$f(x_1, …, x_n)$。拉格朗日函数和前文一样，除了每个约束有不同的$\lambda$。
约束：

$L(x_1, ..., x_n, \lambda_1, ..., \lambda_k) = f(x_1, ..., x_n) - \sum_{j=1}^k \lambda_j g_j(x_1, ..., x_n)$

(我们将$j$用于$k$作为约束索引，将$i$用于$n$作为变量的索引$x_i$。)约束最小值出现在所有变量对$L$的偏导数为零的点上。

简单例子

我们将使用一个相对简单的例子来说明方法：我们试图最小化 $x_1^2 + x_2^2 + x_3^2$
有两个约束条件：$x_1 = 1$ 和 $x_2 = 1$
Lagrangian: $x_1^2 + x_2^2 + x_3^2 - \lambda_1 (x_1 - 1) - \lambda_2 (x_2 - 1)$
它的偏导数是：

$\begin{array}{rcl} \partial L / \partial x_1 &=& 2 x_1 - \lambda_1 \\ \partial L / \partial x_2 &=& 2 x_2 - \lambda_2 \\ \partial L / \partial x_3 &=& 2 x_3 \\ \partial L / \partial \lambda_1 &=& -(x_1 - 1) \\ \partial L / \partial \lambda_2 &=& -(x_2 - 1) \end{array}$

解

将它们全部设置为零得到答案：$(x_1, x_2, x_3) = (1, 1, 0)$ 和 $\lambda_1 = \lambda_2 = 2$.

在一个约束情形中，拉格朗日乘子方程等价于矢量方程 $\nabla f = \lambda \nabla g$
对于多个约束，相应的向量方程是：

$\nabla f = \sum_{j = 1}^k \lambda_j \nabla g_j$

解释

上述等式将得出以下事实：对于变量 $i$，当 $\partial L / \partial x_i = \partial f / \partial x_i - \sum_{j=1}^k \lambda_j \partial g_j / \partial x_i$ 成立时有 $\partial f / \partial x_i = \sum_{j=1}^k \lambda_j \partial g_j / \partial x_i$ ，因此把 $\partial L / \partial x_i$ ($i$从$1$到$n$)偏导数置为零等效于上述向量方程。注意，将偏导数$\partial L / \partial \lambda_j$等于零只会强化$g_j(x_1, …, x_n) = 0$的约束。

如何相切

在一个约束情形中，找到点是有用的， $\nabla f = \lambda \nabla g$因为这意味着水平曲线$f$ 与水平曲线$g$相切。在多重约束的情况下，它并不那么简单。单个约束$g_i$的水平表面不一定与$f$约束最小值处的水平表面相切。（在上面的示例中，约束平面$x_1 = 1$与$f$球体的水平面$x_1^2 + x_2^2 + x_3^2 = 2$在最佳点处相交$(1, 1, 0)$。）相反，事实证明，所有$g_i$水平面的交点都与$f$水平面的相切。

为了更好的理解，让我们直接看$x$的小扰动对 $f$和约束方程$g_j$的影响，有$x = (x_1, …, x_n)$，同时使$\Delta x = (\Delta x_1, …, \Delta x_n)$我们有：

$f(x + \Delta x) - f(x) \approx \sum_{i=1}^n \Delta x_i \frac{\partial f}{\partial x_i}$

条件

如果更改$x$，有扰动$\Delta x$ 能保持所有$g_j$约束方程有相同的（一阶导），同时引起$f(x)$的非零变化，则$x$不可能是受约束的局部最小值。因为在某些方向上沿的交点移动所有的水平曲线$g_j$都会导致$f$减少（或增加）。所以我们想要的条件是：

对于所有可能使 $\nabla g_j(x) \perp \Delta x$ ,($j$从$1$到$k$) 成立的 $\Delta x$，有$\nabla f(x) \perp \Delta x\textrm{.}$

对每个$j$有$\nabla g_j(x) \perp \Delta x$, $\Delta x$在与$g_j$水平面相切的方向上。如果$\Delta x$在与所有的$g_j$水平面交点相切的方向上，那么每一个$j$都成立。条件一表示任何此类$\Delta x$也与水平面相切$f$。另一方面，拉格朗日乘子法强制执行的条件是：

存在 $\lambda_1$ 到 $\lambda_k$ 使得 $\nabla f = \sum_{j = 1}^k \lambda_j \nabla g_j$ .

令人高兴的是，事实证明条件1和2等价。

定理：条件1和2等价

证明

证明:(为什么现在我们一整天挥手都有严格的证据？有时最直观的论证就是证明;也许就是这种情况。）首先我们将证明2、1等价.假设对于每一个 $j$ 从 $1$ 到 $k$ ，有 $\nabla f = \sum_{j = 1}^k \lambda_j \nabla g_j$ , $\nabla g_j(x) \perp \Delta x$ 。因为 $\nabla g_j(x) \perp \Delta x$, $\nabla g_j(x) \cdot \Delta x = 0$ 。所以 $\nabla f \cdot \Delta x = (\sum_{j = 1}^k \lambda_j \nabla g_j) \cdot \Delta x = \sum_{j = 1}^k \lambda_j \nabla g_j \cdot \Delta x = 0.$ 。这意味着 $\nabla f \perp \Delta x$ 。

接下来我们将证明1意味着2，或等效地，不是2意味着不是1.否定2表示$\nabla f$不在向量的跨度内。让我们用$z$来表示 $\nabla f$ 在 $\nabla g_j$ 跨度内的投影，并设置$\Delta x = \nabla f - z$。我们将证明这是建立否定条件1的反例。

证否

我们知道 $\nabla f \neq z$ 所以有 $\Delta x \neq 0$，通过投影的定义，对每个$j$有$\Delta x \perp g_j$。此外，$\nabla f \cdot \Delta x = (z + \Delta x) \cdot \Delta x = z \cdot \Delta x + \Delta x \cdot \Delta x$，因为 $z$ 是在$g_j$域上垂直于$\Delta x$，同样的有$z \perp \Delta x$。
新增$z \cdot \Delta x = 0$ 和$\Delta x \cdot \Delta x \neq 0$ ，我们得到 $(z + \Delta x) \cdot \Delta x \neq 0$。也就是说$\nabla f \cdot \Delta x \neq 0$，所以$\nabla f$不垂直$\Delta x$。由于$\Delta x$垂直于所有$\nabla g_j$，但不垂直$\nabla f$，所以条件一也被证否。我们假设条件2的否定，因此这表明不是2意味着不是1，或者等效地，1意味着2。

小结

现在我们已经看到拉格朗日乘子法通过找到 $x$ 一组 $\lambda_j$ 这样 $\nabla f = \sum_{j = 1}^k \lambda_j \nabla g_j$ 的东西而发挥作用。这个等式意味着不存在局部变化，使一阶导数，符合所有约束但改变目标函数 $f$ 的值。因此满足该等式的值$x$是受约束的局部最小值或最大值的候选值。求解该向量方程等效于将拉格朗日函数的偏导数设置为零。

我希望能够说明拉格朗日乘子法的工作方式和原因，并稍使它们看起来不这么像魔术。

后记

感觉原文作者描述的非常严谨，有很多地方我没法跟上作者的思路。
就我个人较感性的理解

单约束的表达式中：

$L(x, y, \lambda)= f(x，y) - \lambda g(x, y)$

拉格朗日函数偏导为零，表明梯度$\nabla f=(\frac{\partial f}{\partial x}, \frac{\partial f}{ \partial y}) $ ，和梯度 $\nabla g=(\frac{\partial g}{\partial x}, \frac{\partial g}{ \partial y}) $ 成比例。
只有在切点处才有梯度重叠，才可以向量互相线性表示；
在切点处是局部的极值点，任何符合$g$的微小扰动$(\Delta x, \Delta y)$ 会导致函数$f$的增大或减小。
所以解$L$偏导等于零的方程组(2+1)，可以得到候选极值点。

在多约束表达式中：

$L(x_1, ..., x_n, \lambda_1, ..., \lambda_k) = f(x_1, ..., x_n) - \sum_{j=1}^k \lambda_j g_j(x_1, ..., x_n)$

有多变量，多约束条件；可以认为是求解极值向量的问题
多约束的条件下，单条件相切并不一定是局部极值；
需要做到$f$与所有$g_i$的相交处相切，即在约束面上各方向目标函数偏导数为零处。
梯度的原理同单约束，梯度向量在各方向上成比例。

$\begin{pmatrix} \lambda_1 \\ \lambda_2 \\ ...\\ \lambda_k \\ \end{pmatrix}^T .\begin{pmatrix} \nabla g_1\\ \nabla g_2 \\ ...\\ \nabla g_k \\ \end{pmatrix}=\nabla y$

在局部最优解的向量上，符合所有约束$g$的微小扰动向量$(\Delta x_1, \Delta x_2, …\Delta x_n)$都会导致函数$f$的增大或减小。
所以解$L$偏导等于零的方程组(n+1)，可以得到候选极值向量。

$g(x_1, x_2, z_3) = x_1^2 + x_2^2 + x_3^2 \\ x_1^2 + x_2^2 + x_3^2 = 2 \\ x_1 = 1 \\ x_2 = 1$

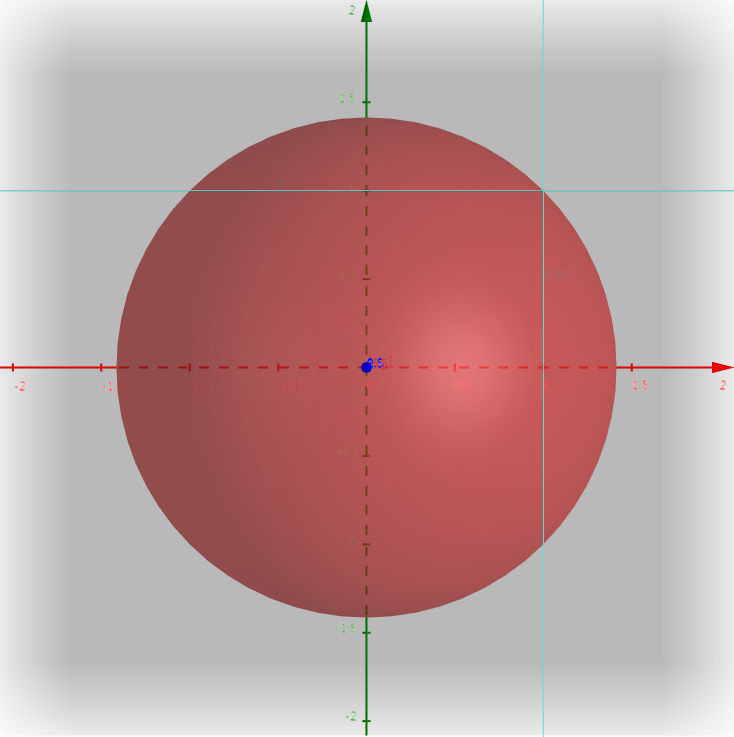
将目标函数约束到三维空间，超平面中的球体半径为所求目标函数的值。

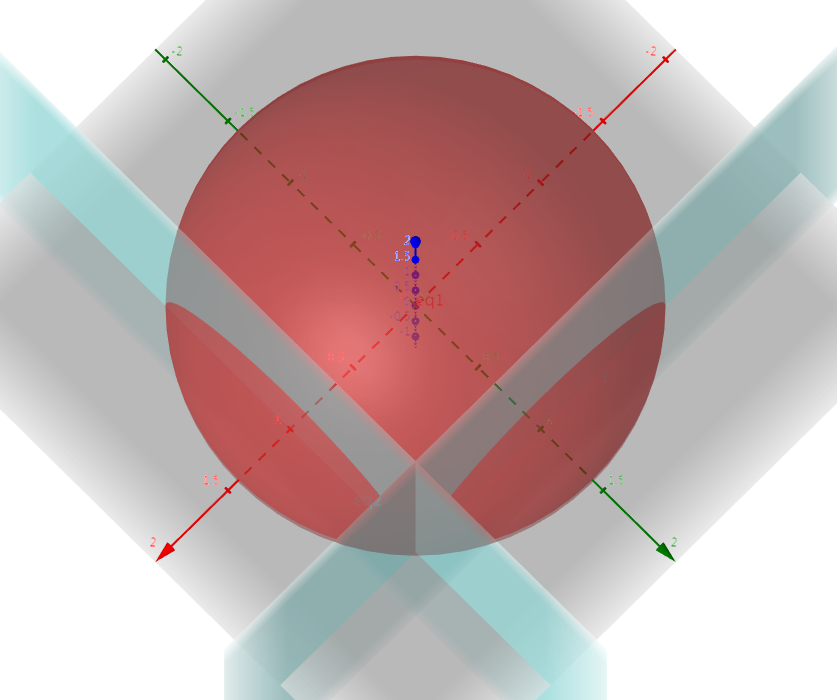
在$(1, 1, 0)$处球体与约束平面相切，取到极值2。

https://danstronger.wordpress.com/2015/08/08/lagrange-multipliers/
https://jermmy.github.io/2017/07/27/2017-7-27-understand-lagrange-multiplier/
https://www.svm-tutorial.com/2016/09/duality-lagrange-multipliers/