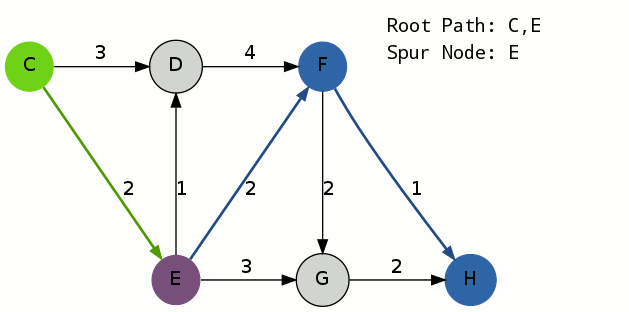
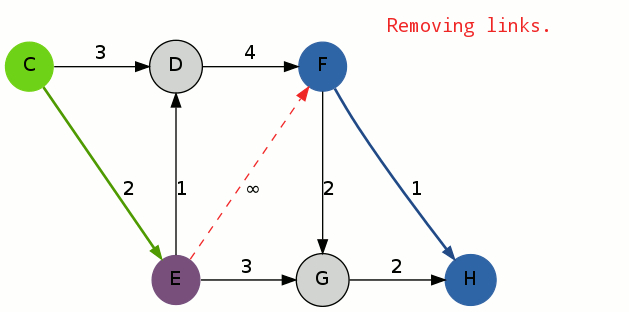
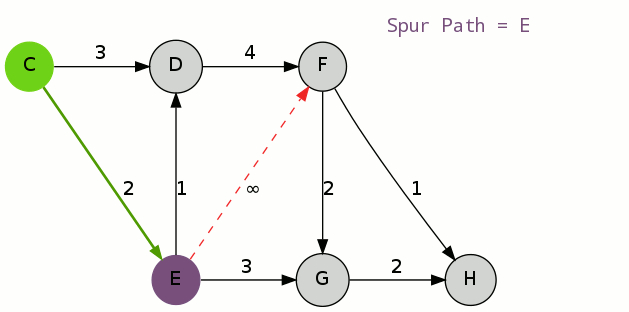
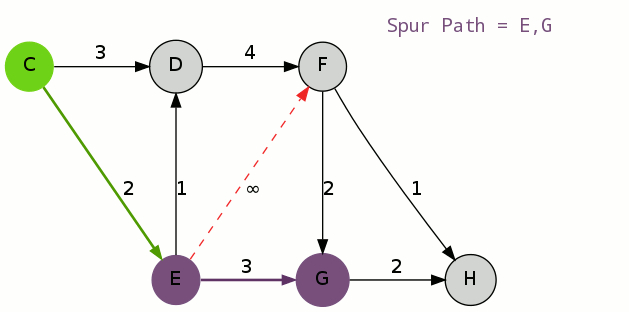
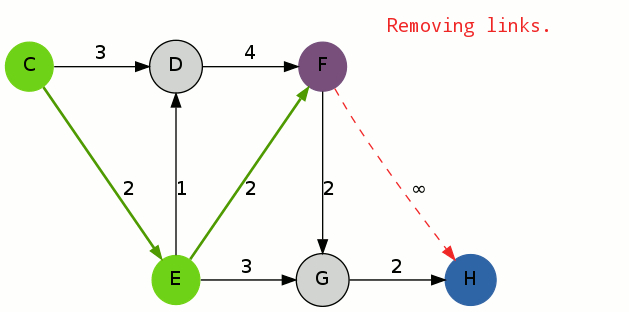
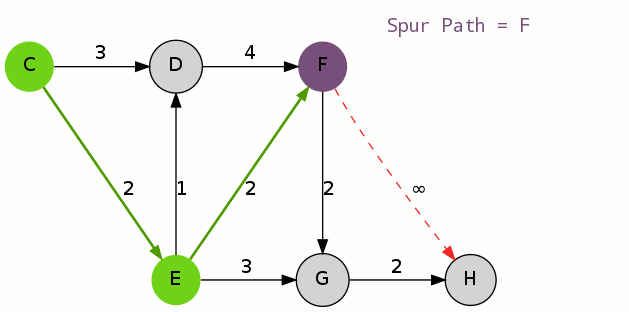
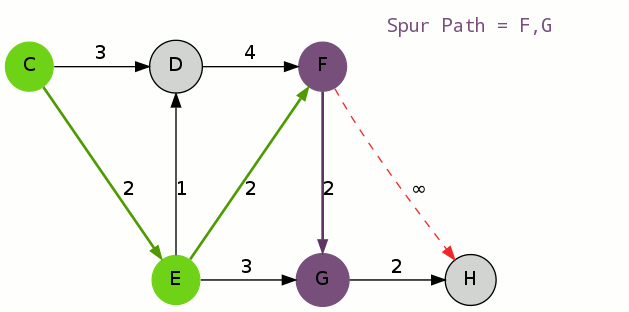
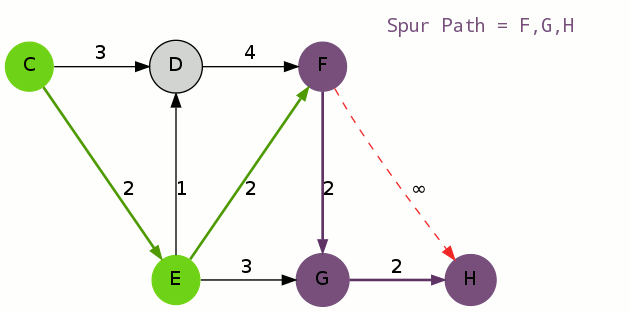
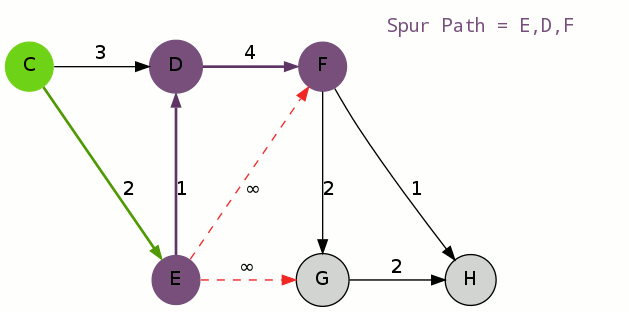
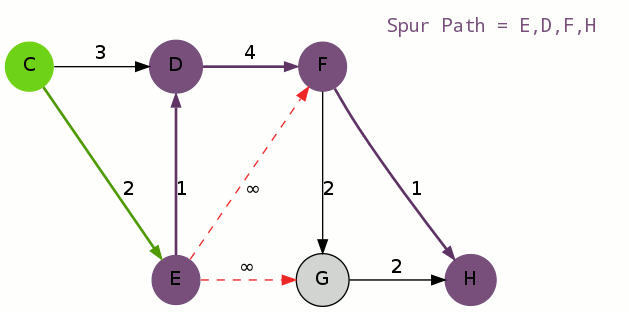
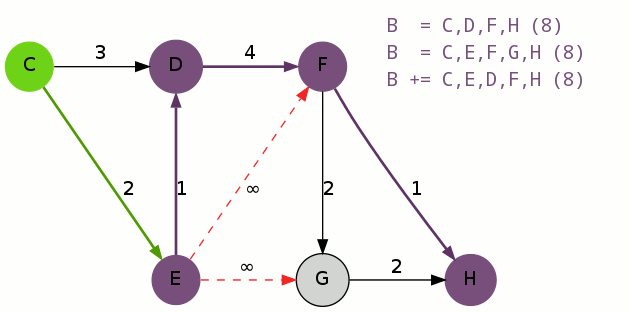
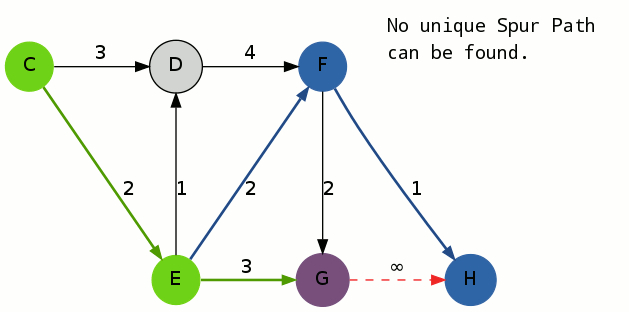
初等变换将矩阵化为最简形

求可逆矩阵P,使PA化为行最简形

矩阵A行列式不为0，矩阵变换 (AE) -> (EP)

设$$

\begin{vmatrix}
-5 & 3 & 1\
2 & -1 & 1
\end{vmatrix}

(AE) = \begin{vmatrix}
-5 & 3 & 1 & 1 & 0\
2 & -1 & 1 & 0 & 1
\end{vmatrix}

• 求可逆矩阵Q,使$QA^T$化为行最简形

利用矩阵初等变换，求方阵的逆矩阵$\begin{vmatrix} 3 & 2 & 1\\ 3 & 1 & 5\\ 3 & 2 & 3\end{vmatrix}$

求X，使AX=B

初等行变换
$P(A, B) ~ (F, PB)$ 当F为单位矩阵时，P为A的逆矩阵即： $P(A, B) ~ (E, A^{-1}B)$

• $$A = \begin{vmatrix} 4 & 1 & -2\\ 2 & 2 & 1\\ 3 & 1 & -1 \end{vmatrix}$$ $$B = \begin{vmatrix} 1 & -3\\ 2 & 2\\ 3 & -1 \end{vmatrix}$$

求X，使XA=B

初等列变换
$P(A top B) ~ (F top PB)$当F为单位矩阵时，P为A的逆矩阵即：$P(A top B) ~ (E top A^{-1}B)$

• $$A = \begin{vmatrix} 0 & 2 & 1\\ 2 & -1 & 3\\ -3 & 3 & -4 \end{vmatrix}$$ $$B = \begin{vmatrix} 1 & 2 & 3\\ 2 & -3 & 1 \end{vmatrix}$$

k为何值时会有对应个数解？$A = \begin{vmatrix}1 & -2 & 3k\\-1 & 2k & -3\\k & -2 & 3\end{vmatrix}$

1. k=1时 ，秩为1
2. k=-1时， 秩为2
3. k不为1或-1时， 秩为3

$\lambda$取何值时，非齐次线性方程组

1. $\lambda$ 不为1或-2时， 有唯一解
2. $\lambda$ 为-2时， 无解
3. $\lambda$ 为1时， 有无限解

• 如果矩阵A经过有限次行初等变换变为矩阵B，称矩阵A与矩阵B行等价记作 $$A r top \thicksim B$$
• 如果矩阵A经过有限次列初等变换变为矩阵B，称矩阵A与矩阵B列等价记作 $$A c top \thicksim B$$
• 如果矩阵A经过有限次初等变换变为矩阵B，称矩阵A与矩阵B等价记作 $$A \thicksim B$$

变换后的阶梯形线性方程组系数+增广组成矩阵，称为行最简形矩阵
把行最简形矩阵再施以初等变换可以得到更简单的矩阵称为标准形

定义

• 有三种形式的初等变换
  1. 对调两行
  2. 某个数k(非0)乘以某行的所有元素
  3. 某个数k(非0)乘以某行的所有元素， 加到另一行对应元素上
• 由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵
• 在 m x n的矩阵A中取k行k列，其交叉处元素组成的行列式，称为A的k阶子式
• 在矩阵A中如果有r阶非零子式D，而r+1阶为零，称D为A的最高阶非零子式，r称为A的秩，记作R(A)

定理一

1. $A r top \thicksim B$的充分必要条件是存在m阶可逆矩阵P，使PA = B;
2. $A c top \thicksim B$的充分必要条件是存在m阶可逆矩阵Q，使AQ = B;

3. $A \thicksim B$的充分必要条件是存在m阶可逆矩阵P, n阶可逆矩阵Q，使PAQ = B;

4. 性质一: 对矩阵A进行一次初等变换相当于左乘或右乘初等矩阵

5. 性质二: 方阵A可逆的充分必要条件是存在有限个初等矩阵P1 P2 … pn, 使 A = P1 P2 … pn
6. 推论: 方阵A可逆的充分必要条件是$A r top \thicksim E$

定理二

若 $A \thicksim B$，则 R(A) = R(B)
推论： 如果可逆矩阵P、Q，可使 PAQ = B， 则R(A) = R(B)

1. $$0 \leqslant R(A_{m*n}) \leqslant min\{m, n\}$$
2. $$R(A^T) = R(A)$$
3. $$IF \quad A \thicksim B \quad THAN \quad R(A) = R(B)$$
4. 如果 P、Q可逆，则：R(PAQ) = R(A)
5. $$max\{R(A), R(B)\} \leqslant R(A, B) \leqslant R(A) + R(B)$$
6. $$R(A+B) \leqslant R(A) + R(B)$$
7. $$R(AB) \leqslant min\{R(A), R(B)\}$$
8. $$IF \quad A_{m*n}B_{n*l} = O \quad THAN \quad R(A) + R(B) \leqslant n$$

定理三

对于n元线性方程组Ax = b

1. 无解的充分必要条件是 R(A) < R(A, b), 系数矩阵的秩小于增广矩阵的秩
2. 有唯一解的充分必要条件是 R(A) = R(A, b) = n, 标准形等于行数
3. 有无限解的充分必要条件是 R(A) = R(A, b) < n, 标准形低于行数

定理四

n元齐次线性方程组 Ax = 0 有非零解的充分必要条件是 R(A) < n (3.3)

定理五

线性方程组 Ax = b 有解的充分必要条件是 R(A) = R(A, b) (3.2)

定理六

线性方程组 Ax = B 有解的充分必要条件是 R(A) = R(A, B) (3.2)

1s -> 10^3ms -> 10^6us -> 10^9ns

1. cpu's speed depend on frequency, one 3Gz core can execute 3x10^9 command
   convert to time, one command need about 0.33ns. To human like a blink 0.4s.
2. level-1 cache read once need 0.5ns, to human like a heart beat 1.3s
3. branch predict need 5ns, about 13s to human
4. level-2 cache read once need 7ns, about 18.3s to human
5. mutex-lock lock or unlock need 25ns, about a minute to human
6. memory address searching need 100ns, about 4 minute to human
7. cpu switch context need 1500ns (1.5us), about a hour to human
8. transfer data in a 1Gpbs web 2kb need 20us, about 14.4h to human
9. SSD random read need 120us, about 4.5d to human
10. read data from meory a sequencial 2mb data need 250us, about 7.5d to human
11. SSD read data a sequencial 1mb data need 1ms, about a month to human
12. hard disk read a sequencial 1mb data need 20ms, about 20 month to human
13. different world web a ping need 120ms, about 12.5 year to human
14. reboot vm need 4s, about 300y to human
15. reboot machine need 5minute, about 25000y……

Definitions

• G represent a graph
• P represent a path
• s represent source start vertex
• w(u, v) mean edge weight from vertex u to v
• d(u, v) mean short path cost from vertex u to v

Algorithm

1. Find shortest path P1
2. Recalculate the edge weith by w′(u,v) = w(u,v) − d(s,v) + d(s,u)
3. Create a residual graph Gt formed from G by removing the edges of G on path P1 (leave a reserve zero path)
4. Find the shortest path P2 in the residual graph Gt
5. Discard the reversed edges of P2 from both paths

The remaining edges of P1 and P2 form a subgraph have no common edges.
Return the two disjoint paths from the subgraph.

Example

• Figure A illustrates a weighted graph G.
• Figure B calculates the shortest path P1 from A to F (A–B–D–F).
• Figure C illustrates the shortest path tree T rooted at A, and the computed distances from A to every vertex (u).
• Figure D shows the residual graph Gt with the updated cost of each edge and the edges of path ‘P1 reversed.
• Figure E calculates path P2 in the residual graph Gt (A–C–D–B–E–F).
• Figure F illustrates both path P1 and path P2.
• Figure G finds the shortest pair of disjoint paths
  Combining the edges of paths P1 and P2 and then discarding the common reversed edges between both paths (B–D).
  As a result, we get the two shortest pair of disjoint paths (A–B–E–F) and (A–C–D–F).

https://en.wikipedia.org/wiki/Suurballe%27s_algorithm

K shortest path problem have three ideas:

• recurrence method
  based on P(i), recurrent resolve the P(i+1) shortest path.
• direct method
  direct find the shortest path, like delete method.
• synthetic method
  i have no idea yet.

Yen’s algorithm computes single-source K-shortest loopless paths for a graph with non-negative edge cost.
The algorithm was published by Jin Y. Yen in 1971 and employs any shortest path algorithm to find the best path,
then proceeds to find K − 1 deviations of the best path.

Reference

http://www.coolee.me/yen-k-shortest-path.html
https://en.wikipedia.org/wiki/Yen%27s_algorithm

矩阵乘法

设

求$3AB-2A$及$A^TB$

举反例证明以下命题是错的

• 如果$A^2=\omicron$则$A=\omicron$ $$A = \begin{pmatrix} 1 & 1 \\ -1 & -1 \end{pmatrix}$$
• 如果$A^2=A$则$A=\omicron$或$A=E$ $$A = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}$$
• 如果$AX=AY(A \neq \omicron)$则$X=Y$ $$A = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} X = \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix} Y = \begin{pmatrix} 1 & 0 \\ 0 & 3 \end{pmatrix}$$

矩阵的转置

• A、B是n阶矩阵，A是对称矩阵，则$B^TAB$也是对称矩阵 $$(B^TAB)^T = (AB)^TB = B^TAB$$
• A、B是n阶对称矩阵，AB是对称矩阵的充分必要条件是AB=BA $$AB = (AB)^T = B^TA^T = BA$$

求矩阵的逆矩阵：

求矩阵X

推导

• 设A为3阶矩阵，$|A|=\frac{1}{2}$， 求$|(2A)^{-1} - 5A^* |$

• 设$A = \begin{pmatrix} 0 & 3 & 3 \\ 1 & 1 & 0 \\ -1 & 2 & 3 \end{pmatrix}$， AB = A + 2B， 求B

• 设 $$A = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 2 & 0 \\ 1 & 0 & 1 \end{pmatrix}$$ 且$AB + E = A^2 + B$， 求B

• 设A = diag(1, -2, 1)， $A* BA = 2BA-8E$， 求B

• 已知矩阵A的伴随矩阵A*为diag(1, 1, 1, 8)， 且$ABA^{-1} = BA^{-1} + 3E$， 求B

二项式

• 设
  $P^{-1}AP = \Lambda$， $P = \begin{pmatrix} -1 & -4 \\ 1 & 1 \end{pmatrix}, \Lambda = \begin{pmatrix} -1 & 0 \\ 0 & 2 \end{pmatrix}$， 求A^11

• 设 $$AP = P\Lambda$$

求$\varphi(A) = A^8(5E - 6A + A^2)$

矩阵分块法

• $$\begin{pmatrix} 1 & 2 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 3 & 1 \\ 0 & 1 & 2 & -1 \\ 0 & 0 & -2 & 3 \\ 0 & 0 & 0 & -3 \end{pmatrix}$$

• $\begin{pmatrix} 3 & 4 & 0 & 0 \\ 4 & -3 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 2 & 2 \\ \end{pmatrix}$， 求|A^8|及A^4

Matrix

概念

A称作m x n矩阵，矩阵中的数称作矩阵A的元。
$a_{ij}$位于矩阵的第i行，j列，称作矩阵A的(i, j)元。

• 行列均为n的矩阵成为n阶矩阵或n阶方阵；
• 只有一行的矩阵成为行向量
• 只有一列的矩阵成为列向量。
• 行列相同的两矩阵成为同型矩阵
• 矩阵的元均是0的矩阵成为零矩阵

线性变换

从 $x_1 , x_2 , ... x_n$到$y_1 , y_2 , ... y_n$的过程称作线性变换

n阶方阵，主对角线均为1的矩阵，称作单位矩阵E。
代表这线性变换中的恒等变换，$x_i -> y_i$

Arithmetic

加减

有矩阵$A = (a_{ij}), B = (b_{ij})$同型矩阵则：

矩阵加减满足交换率、结合律

1. A + B = B + A
2. (A + B) + C = A + (B + C)

乘法

数乘矩阵：

1. $$(\lambda \mu)A = \lambda (\mu A)$$
2. $$(\lambda + \mu) A = \lambda A + \mu A$$
3. $$\lambda(A + B) = \lambda A + \lambda B$$

矩阵相乘：
有矩阵$A = (a_{ij})$是m s的矩阵，$B = (b_{ij})$是s n的矩阵,$C = (c_{ij})$：

只有A矩阵的列和B矩阵的行相同时才能相乘
把矩阵相乘记作AB = C，C中的元即是A的行元与B的列元的积和。

1. $$(AB)C = A(BC)$$
2. $$\lambda(AB) = (\lambda A)B = A(\lambda B)$$
3. $$A(B + C) = AB + AC, (A + B)C = AC + BC$$

n阶方阵，主对角线均为$\lambda$的矩阵，称作纯量矩阵

矩阵乘法一般不满足交换律，开平方公式、平方和公式，只有在AB可交换是有效。

矩阵的转置

将矩阵元放入行列交换的位置形成的新矩阵，称为转置矩阵$A^T$

1. $$(A^T)^T = A$$
2. $$(A + B)^T = A^T + B^T$$
3. $$(\lambda A)^T = \lambda A^T$$
4. $$(AB)^T = B^TA^T$$

方阵行列式

1. $$\lvert A^T \rvert = \lvert A \rvert$$
2. $$\lvert \lambda A \rvert = \lambda^n \lvert A \rvert$$
3. $$\lvert AB \rvert = \lvert A \rvert \lvert B \rvert$$

关于第一点可参考行列式性质一，转置的行列式的组合与未转置的行列式一一对应。

伴随矩阵 为原矩阵元的代数余子式所组成的矩阵的转置

由于原矩阵的行和其伴随阵列的积，即行元对应代数余子式的和即是行列式的值D。
矩阵相乘，不在同行的积为0，所以最后得到的是一个纯量矩阵

Inverse matrix

给出一线性变换：

设X为xi组成的向量，Y为yi组成的向量， A为系数矩阵：

左乘A的伴随矩阵得到：

当A的行列式不为0时，有

设$B = \frac{1}{\lvert A \rvert} A^*$， 则有$X = BY$

• 如果对n阶矩阵A，有矩阵B使 AB=BA=E, 则称B为A的逆矩阵
• 如果矩阵A可逆，则$\lvert A \rvert \neq 0$
• 如果$\lvert A \rvert \neq 0$, 则矩阵A可逆

• 如果A可逆，则$A^{-1}$也可逆。$(A^{-1})^{-1} = A$
• 如果A可逆，$\lambda \neq 0$，则$\lambda A$也可逆。$(\lambda A)^{-1} = \frac{1}{\lambda} A^{-1}$
• 如果A、B为同阶矩阵均可逆，则AB也可逆。$(AB)^{-1} = B^{-1}A^{-1}$

polynomial 多项式

1. 如果$A = P \Lambda P^-1$ 则 $A^k = P \Lambda^k P^-1$

   $$\varphi(A) = a_0E+a_1A+...a_mA^m$$ $$= Pa_0EP^{-1} + Pa_1AP^{-1}+...Pa_mA^mP^{-1}$$ $$= P\varphi(\Lambda)P^{-1}$$

2. 如果$\Lambda = diag(\lambda_1, \lambda_2...\lambda_n)$是对角阵,则有$\Lambda^k = diag(\lambda_1^k, \lambda_2^k...\lambda_n^k)$

   $$\varphi(\Lambda) = a_0E + a_2\Lambda + ... a_m\Lambda^m$$

Matrix block

• 矩阵A、B有相同行列数、分块方法有： $$A = \begin{pmatrix} A_{11} & ... & A_{1r}\\ ... & ... & ... \\ A_{s1} & ... & A_{sr} \end{pmatrix}, B = \begin{pmatrix} B_{11} & ... & B_{1r}\\ ... & ... & ... \\ B_{s1} & ... & B_{sr} \end{pmatrix}$$

*

是分好块的矩阵， $\lambda$是一个数，则有：

• A 为m x l矩阵，B为l x n, 分块同上，则有： $$AB = \begin{pmatrix} C_{11} & ... & C_{1r}\\ ... & ... & ... \\ C_{s1} & ... & C_{sr} \end{pmatrix}$$

ps. A矩阵为s x t，B矩阵为t x r。

• 设$A = \begin{pmatrix} A_{11} & ... & A_{1r}\\ ... & ... & ... \\ A_{s1} & ... & A_{sr} \end{pmatrix}$，则$A^T = \begin{pmatrix} A_{11}^T & ... & A_{1r}^T\\ ... & ... & ... \\ A_{s1}^T & ... & A_{sr}^T \end{pmatrix}$
• 如果A为n阶矩阵，如果A的分块只有在主对角线上有非零子块，称A为分块对角矩阵

jps (JVM Process Status Tool)

Used to check progress id/ start path/ start argument.
If remote machine running jstat, jps can query remote vm progress.
define:
jps [-q] [-mlvV] [<hostid>]

• -m arguments that input into main
• -v arguments that input into jvm
• -l main class package path or jar file path

jmap( Memory Map for Java)

mapping jvm’s object/ reference
define:
jmap [option] <pid>

1
2
3

jmap -histo 20836
jmap -permstat 20836
jmap -dump:live,format=b,file=data.hprof 20836

jhat(JVM Heap Analysis Tool)

offline dump file analysis, check memory info.
But Visual interface is much more better like jvisualvm jconsole

jinfo(Configuration Info for Java)

print or modify java progress’s options(flag). print system properties

1
2

jinfo -sysprops 20836
jinfo -flags 20836

jstat(JVM statistics Monitoring Tool)

monitor jvm grogress’s resource and performence
define:
jstat -<option> [-t] [-h<lines>] <vmid> [<interval> [<count>]]

Troubleshooting

Local Applications Cannot Be Monitored (Error Dialog On Startup)
Description: An error dialog saying that local applications cannot be monitored
is shown immediately after VisualVM startup. Locally running Java applications
are displayed as (pid ###).

Resolution: This can happen on Windows systems if the username contains capitalized letters.
In this case, username is UserName but the jvmstat directory created by JDK is %TMP%\hsperfdata_username.
To workaround the problem, exit all Java applications, delete the %TMP%\hsperfdata_username directory
and create new %TMP%\hsperfdata_UserName directory.

In windows platform if jconsole.exe interface, the local vm disenable, check user name, and directory name:

1
2
3
4

# If user name is Administrator
C:\Users\Administrator\AppData\Local\Temp\hsperfdata_administrator
# change to
C:\Users\Administrator\AppData\Local\Temp\hsperfdata_Administrator

https://visualvm.github.io/troubleshooting.html#jpswin2

jstack(Stack Trace for Java)

print specific progress’s or remote jvm’s stack info

Links

http://blog.sina.com.cn/s/blog_b0e3dfe30102wfl5.html

http://www.bubuko.com/infodetail-792105.html

https://www.cnblogs.com/lishijia/p/5897236.html

http://www.talkwithtrend.com/Article/161055

https://www.ibm.com/developerworks/cn/java/j-lo-JVMGarbageCollection/

https://www.ibm.com/developerworks/cn/java/l-JavaMemoryLeak/

Kramo rule

如果线性方程组的系数行列式不等于零，则方程组有唯一解

就方程组右边常数项b1 b2 … bn替换行列式列得到：

定理4 如果线性方程组系数行列式$D \neq 0$，则方程组一定有解，且解唯一

定理4’ 如果方程组无解，或有两个以上的解，则方程组的行列式系数必为零

定理5 如果齐次线性方程组的系数行列式$D \neq 0$，则方程组没有非零解

定理5’ 如果齐次线性方程组有非零解，则方程组的行列式系数必为零

Exercise

• $$\begin{vmatrix} 4 & 1 & 2 & 4 \\ 1 & 2 & 0 & 2 \\ 10 & 5 & 2 & 0 \\ 0 & 1 & 1 & 7 \end{vmatrix}$$

*

求代数余子式

系数替换对应行列式上的行：

*

$b_{34}$总是-1，排列位的和是奇数，与其代数余子式的符号相销得到：

而$b_{33}$总是x，排列位的和是偶数，与余子式相等得到：

交换r1 - r2, c1 - c2，可形成上三角型形式，可得：

根据归纳法可得：

*

形成下三角型行列式，得到：

• $$\begin{cases} 5x_1 &+& 6x_2 & & & & &= 1\\ x_1 &+& 5x_2 &+& 6x_3 & & & = 0\\ & & x_2 &+& 5x_3 &+& 6x_4 & = 0\\ & & & & x_3 &+& 5x_4 & = 1 \end{cases}$$

Expand by row(column)

表达

把n阶行列式i行j列的元素划掉后剩下n-1阶行列行列式称为$a_{ij}$的余子式记作$M_{ij}$

加上符号变化，得到(i, j)元的代数余子式：

引理 一个n阶行列式，如果第i行的元素除了(i, j)元$a_{ij}$外都为0，那么行列式等于$a_{ij}$和它的代数余子式的乘积

• 当(i, j)元是(1, 1)时有：

  $$\begin{vmatrix} a_{11} & 0 & ... & 0\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{31} & a_{32} & ... & a_{3n} \end{vmatrix}$$

  参照例10，右上角为0时，行列式等于主对角两行列式的积：

  $$D = a_{11}M_{11}$$ $$A_{11} = (-1)^2M_{11}$$ $$D = a_{11}A_{11}$$

• 当(i, j)为一般情况时有：

  $$\begin{vmatrix} a_{11} & ... & a_{1j} & ... & a_{1n}\\ ... & ... & ... & ... & ... \\ 0 & ... & a_{ij} & ... & 0\\ ... & ... & ... & ... & ... \\ a_{n1} & ... & a_{nj} & ... & a_{nn} \end{vmatrix}$$

  将(i, j)元对换到(1, 1)位，需要i + j - 2次对换。

  $$D_1 = (-1)^{(i + j - 2)}D = (-1)^{(i + j)}D$$

  替换到(1, 1)元原行列式变号。所得的余子式，即是(i, j)元的余子式

  $$D = (-1)^{(i + j)}D1 = (-1)^{(i + j)}a_{ij}M_{ij} = a_{ij}A_{ij}$$

  根据(1, 1)元的结果，$D1 = a_{ij}M_{ij}$
  $M_{ij}$的变号结果与之前的“换行”变号相销，即得到相同结论。

定理3 行列式等于它的任一行（列）的元素与其对应代数余子式的乘积和

将i行所有元素都表示为(i, k)元加n-1个0，根据性质5，展开n个行列式。
再根据之前的引理，即可得到：

或是：

范德门德行列式(Vandermonde)

式子中的符号代表所有同类因子的乘积。
当n=2时，行列式结果为 $x_2-x_1$ 符合结论。

当一般情况时，将行列式降阶。将后一行减去前一行的x1倍得到：

按第一列展开，将公因子$x_i-x_1$提出：

右端是n-1阶范德门德行列式，按归纳法有：

递推过程中会将$x_i-x_j$的所有组合乘一遍，所得即是全体同类因子的乘积

推论 行列式某一行（列）元素与另一行（列）元素的对应代数余子式乘积只和等于零

将行列式$D = det(a_{ij})$，按第j行展开有：

将aj行换成ai行将导致有两行元素相同，导致行列式等于零。